Matematika kadang kala terasa rumit dan membingungkan bagi banyak orang. Matematika sering kali dipandang sebagai ilmu yang payah, penuh rumus, dan jauh dari kehidupan nyata. Namun siapa sangka, di balik rumus dan angka-angka yang kaku itu, terdapat keindahan dan keteraturan yang mengagumkan. Salah satu contoh terbaik dari keindahan matematika yang sederhana namun luar biasa adalah Deret Fibonacci.
Deret ini bukan sekadar pelajaran matematika di sekolah, melainkan cerminan bagaimana pola bekerja secara alamiah di alam dunia nyata. Ia menunjukkan bahwa matematika tak hanya hidup di buku teks, tetapi juga di bunga yang mekar, di pola daun yang tumbuh, bahkan dalam galaksi yang berputar.
Deret Fibonacci dinamai dari Leonardo da Pisa, seorang matematikawan Italia yang lebih dikenal dengan sebutan Fibonacci. Ia memperkenalkan deret ini ke dunia Barat pada tahun 1202 dalam bukunya yang berjudul Liber Abaci (Buku Penghitungan). Meski konsepnya sudah dikenal di dunia Timur seperti India jauh sebelumnya, Fibonacci memperkenalkan cara penggunaannya untuk menyelesaikan masalah praktis.
Deret Fibonacci adalah urutan angka di mana mulai angka ketiga adalah hasil penjumlahan dari dua angka sebelumnya. Deret ini dimulai dengan 0 dan 1, sehingga menjadi 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
F(n) = F(n-1) + F(n-2)
Dengan ketentuan awal: F(0)=0 dan F(1)=1
Deret ini tampak sederhana, namun memiliki pola dan keteraturan yang menakjubkan. Salah satu keunikannya adalah bahwa semakin besar angka-angka dalam deret ini, rasio antara dua angka yang berurutan akan mendekati suatu nilai konstan, yaitu 1.6180339887…, yang dikenal sebagai rasio emas (golden ratio). Rasio emas ini disimbolkan dengan huruf Yunani φ (phi), dan sering dianggap sebagai angka paling indah dalam matematika karena proporsinya muncul dalam arsitektur klasik, lukisan karya Da Vinci, pada makhluk hidup, bahkan pada anatomi tubuh manusia.
Salah satu alasan mengapa deret Fibonacci begitu mempesona adalah karena pola ini muncul secara alami di banyak hal di dunia nyata, tanpa campur tangan manusia. Beberapa contoh menakjubkan di alam di antaranya [1] Pola bunga dan daun. Banyak bunga memiliki jumlah kelopak yang sesuai dengan angka Fibonacci. Bunga lili 3 kelopak, buttercup 5, daisy 21 atau 34. [2] Pola pertumbuhan tanaman. Daun, biji bunga matahari, dan cabang pohon sering tumbuh dalam pola spiral Fibonacci yang memaksimalkan pencahayaan dan ruang. [3] Spiral cangkang. Cangkang siput, nautilus, dan bahkan pusaran galaksi mengikuti spiral logaritmik yang sebanding dengan rasio Fibonacci. [4] Buah nanas dan cemara. Pola sisik pada kulitnya juga menunjukkan jumlah barisan Fibonacci. Fenomena ini seolah menunjukkan bahwa alam dijalankan dengan logika matematika yang teratur, dan deret Fibonacci menjadi jembatan antara matematika dan kehidupan.
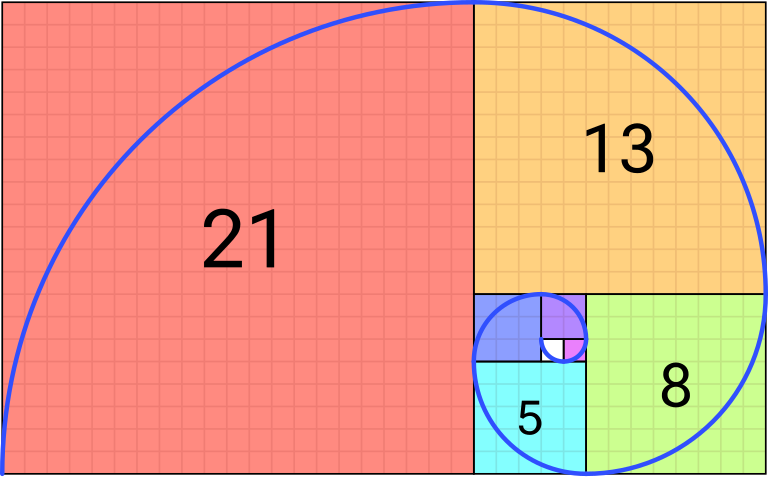
Meskipun terlihat seperti permainan angka yang sederhana, deret Fibonacci muncul dalam berbagai aspek kehidupan dan alam. Urutan Fibonacci muncul dalam berbagai bentuk biologis, mulai dari pertumbuhan tumbuhan hingga bentuk hewan dan bahkan struktur kosmis, mencerminkan desain alami yang efisien dan teroptimasi. Biji-biji di kepala bunga matahari tersusun dalam spiral yang sesuai dengan bilangan Fibonacci, umumnya 21 dan 34 atau 34 dan 55 spiral yang berlawanan arah. Pola ini memungkinkan pengemasan biji yang paling efisien. Cabang pohon yang tumbuh dari batang seringkali sesuai dengan sudut dan jumlah yang terkait dengan rasio emas dan urutan Fibonacci, mengoptimalkan paparan cahaya dan pertumbuhan. Penataan daun di sekitar batang (phyllotaxy) seringkali mengikuti urutan Fibonacci, membantu memaksimalkan paparan cahaya matahari. Banyak bunga memiliki jumlah kelopak yang sama dengan angka Fibonacci. Kamar-kamar cangkang nautilus tumbuh dalam pola spiral yang menyerupai spiral Fibonacci, meskipun bukan spiral rasio emas yang sempurna. Rasio yang terkait dengan urutan Fibonacci muncul dalam proporsi tubuh manusia, dan spiral yang mirip dengan pola Fibonacci ditemukan dalam galaksi dan beberapa perilaku hewan seperti jaring gelembung paus.
Dalam bidang teknologi, deret Fibonacci bukan sekadar keindahan visual, tetapi juga alat yang efisien untuk menyelesaikan berbagai permasalahan teknis. Salah satu aplikasi pentingnya yaitu Algoritma Komputer. Deret Fibonacci sering digunakan untuk memahami konsep rekursi, yaitu teknik pemrograman di mana suatu fungsi memanggil dirinya sendiri. Ini sangat berguna dalam memecah permasalahan besar menjadi lebih kecil.
Deret Fibonacci mungkin tampak sederhana pada awalnya, tetapi di balik kesederhanaannya tersembunyi dunia penuh keajaiban. Deret ini adalah salah satu bukti bahwa matematika bukan hanya soal menghitung, tapi juga tentang menemukan pola, memahami kehidupan, dan menghargai keindahan yang tersembunyi di sekitar kita. Dengan belajar deret Fibonacci, kita tidak hanya belajar angka. Kita belajar cara melihat dunia dengan mata yang lebih tajam dan rasa ingin tahu yang lebih besar.
